Performance assessment of Kriging with partial least squares for high-dimensional uncertainty and sensitivity analysis

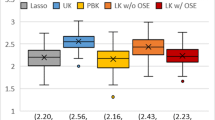
Abstract

This paper aims to assess the potential of Kriging combined with partial least squares (KPLS) for fast uncertainty quantification and sensitivity analysis in high-dimensional problems. Such a fast assessment is especially important in cases that involve a large number of outputs such as uncertain scalar fields or applications in robust and reliability-based optimization. In this regard, the role of the partial least squares is to reduce the dimensionality of the input space to accelerate model construction. We conduct experiments using KPLS on analytical and nonanalytical problems of various complexities and compare various quantities of interest (QOI), i.e., mean, standard deviation, and Sobol sensitivity indices, to those from the original Kriging to perform this assessment. In addition, a comparison with sparse polynomial chaos expansion (PCE) is also performed on nonanalytical problems. Results show that KPLS with four principal components is significantly faster than the ordinary Kriging while yielding comparable accuracy in approximating the statistical moments and Sobol indices. We also observe that KPLS with a proper number of principal components can achieve higher accuracy than Kriging in high-dimensional problems with small sample size, suggesting that the benefit of KPLS is not just on the training time but also accuracy. Finally, we observe no apparent benefits in utilizing KPLS for low-dimensional problems.

Appendix A: Polynomial Chaos Expansion

The nonintrusive version of PCE approximates the black-box function as a sum of orthogonal polynomials $\varvec{\Psi }=\{\Psi _{0},\ldots ,\Psi _{P-1}\}^{T}$ multiplied by the respective coefficients $\varvec{\alpha }=\{\alpha _{0},\ldots ,\alpha _{P-1}\}$, where $\Psi _{i}$ is an individual multidimensional orthogonal polynomial and P is the cardinality of the polynomial basis set $\varvec{\Psi }$. The family of orthogonal polynomial is different for a given distribution $\varvec{\rho }(\varvec{\xi })$, e.g., Legendre and Hermite polynomials are used for uniform and normal distribution, respectively. Formally, a PCE approximation is defined as

$$\begin{aligned} f(\varvec{\xi }) = \sum _{i=0}^{\infty } \alpha _{i}\Psi _{i}(\varvec{\xi }) \approx \sum _{\varvec{\zeta } \in {\mathcal {A}}} \alpha _{i}\Psi _{i}(\varvec{\xi }) \end{aligned}$$

(32)

where $\varvec{\zeta }=\{\zeta _{1},\ldots ,\zeta _{m}\}$, with $\zeta _{i}=0,1,2,\ldots$, is an individual - index and ${\mathcal {A}}_{p} \in {\mathbb {N}}^{m}$ is a multi-index set. The multidimensional individual basis $\Psi _{i}$ itself is the product of one-dimensional orthogonal polynomials, i..e, $\Psi _{\varvec{\zeta }}(\varvec{\xi }) = \psi ^{i}_{\zeta _{1}}(\xi _{1})\times \ldots ,\times \psi ^{m}_{\zeta _{m}}(\xi _{m})$. In this paper, the multi-index set is generated by a hyperbolic truncation technique, i.e., ${\mathcal {A}}_{p,\nu } \equiv \{\varvec{\zeta } \in {\mathbb {N}}^{m}: ||\varvec{\zeta }||_{\nu } \le p\}$ where $|| \varvec{\zeta }||_{\nu } \equiv \big (\sum \nolimits_{i=1}^{m}\zeta _{i}^{\nu } \big )^{1/\nu }$ and $\nu$ is a scalar for hyperbolic truncation in the range of (0, 1]. Notice that using $\nu =1$ equals to the standard total-order truncation while setting $\nu <1$ will reduce the number of polynomial bases in the set.

Calculation of $\varvec{\alpha }$ is done by the standard ordinary least squares (OLS), that is, $\varvec{\alpha } = ({\varvec{F}}^{T}{\varvec{F}})^{-1}{\varvec{F}}^{T}{\varvec{y}}$ where ${\varvec{F}} = \{\varvec{\Psi }^{(1)},\ldots ,\varvec{\Psi }^{(n)}\}$ is the $n \times P$ regression matrix. However, the use of OLS is only possible when $n<m$. The recommended approach is to use the sparse approximation to calculate $\varvec{\alpha }$, in which only the important polynomials that are given the nonzero coefficients. In this paper, we utilize the least-angle regression (LARS) to construct a sparse PCE approximation based on the given polynomial set ${\mathcal {A}}_{p,\nu }$ (Blatman and Sudret 2011), with the parameters are set to $\nu =0.4$ and the order is varied from $p=1$ to $p=8$.